Решение отдельных маркетинговых задач
Содержание
- 7.1. Задачи по определению наличия эффекта воздействия
- 7.2. Определение наличия связи между переменными
- 7.3. Задачи прогноза
- 7.4. Ценовые коридоры
- 7.5. Ранжирование объектов методом попарного сравнения
- 7.6. Многокритериальный выбор
- 7.7. Статистические методы контроля качества
- 7.8. Анализ экспертных оценок
- 7.9. Разработка методов оценки объема рынка для лекарственного средства
- Литература, рекомендуемая к изучению
Жизнь требует, чтобы каждый новый опыт давал хотя и грубый, но быстрый и практический вывод, годный для руководства сейчас или в самом близком будущем. Абсолютно верные заключения, если таковые и достигаются в практической жизни, получаются посредством целого ряда приближенных решений; ведь странно было бы терять время на ожидание этой уверенности в абсолютной правде, когда нужно делать живое дело.
А.Т. Мэхэн
В этом разделе рассматривается ряд маркетинговых задач. Выделены они в отдельный раздел, во-первых, ввиду относительной новизны этого вида деятельности, а во-вторых, в связи с тем, что только отдельные книги по маркетинговым исследованиям уделяют внимание собственно статистическому аспекту анализа данных. Поскольку во многих случаях статистическая обработка принципиально не отличается от примеров, приведенных ранее, здесь подробно не рассматривается решение всех задач — после постановки задачи дается ссылка на подраздел, где было приведено подобное решение или пример. Исключение составляют задачи, которые имеют особенности или не рассматривались ранее.
Следует отметить, что некоторая информация, содержащаяся в данном разделе пригодится не только маркетологам. Так, методы многокритериального выбора и анализа временных рядов достаточно часто применяют специалисты, занимающиеся медико-биологическими исследованиями. Контрольные карты рекомендуется использовать для контроля состояния исследовательского оборудования и поступающих материалов.
7.1. Задачи по определению наличия эффекта воздействия
Одна из достаточно часто встречающихся задач — определение наличия эффекта воздействия и, возможно, его величины. Например, эффект некоторого рекламного воздействия на объем продаж. Или сравнение различных видов рекламы. Использование эффективных рекламных средств обычно стоит дорого, поэтому важно оценить целесообразность применения именно этих средств. Методы, позволяющие осуществить такую проверку, описаны в разделе 3.
Рассмотрим пример. Допустим, у нас имеется сеть аптек по всему городу. Чтобы повысить объем продаж определенного препарата помещена реклама в метрополитене на один месяц. По истечении этого периода нужно принять решение о продолжении или прекращении рекламы препарата в метрополитене. Для этого необходима следующая информация: объемы реализации в каждой аптеке за месяц до начала этого рекламного мероприятия и за период его проведения (табл. 7.1); среднее увеличение объема реализации на одну аптеку, которое обеспечивает окупаемость прибыли (рассчитывается экономистом).
Таблица 7.1
Объем реализации за месяц до и после рекламного воздействия
| Объем реализации, | Номер аптеки | |||||||
| тыс. грн. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Без рекламы
|
13 | 23 | 12 | 11 | 24 | 34 | 32 | 18 |
| С рекламой | 20 | 24 | 11 | 17 | 28 | 34 | 39 | 24 |
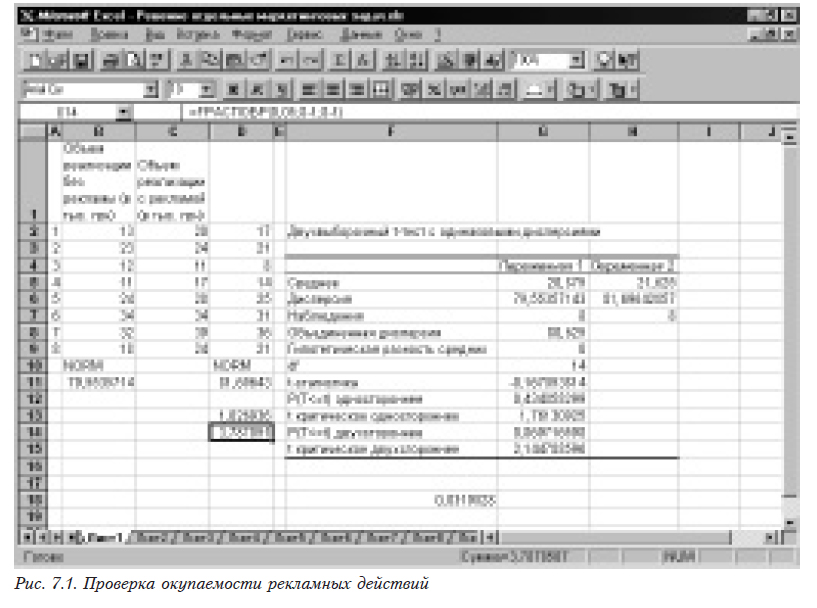
Экономист определил, что необходимое среднее увеличение объема реализации должно составить 3000 грн. Для проверки гипотезы о том, что среднее увеличение реализации в аптеке при рекламировании препарата превышает 3000 грн., необходимо выполнить следующие действия (рис. 7.1).
- От всех значений второго столбца (реализация с рекламой) отнять 3. Для этого в ячейку D2 помещают формулу =C2-3, которую затем размножают на весь столбец.
- Проверяем, можно ли считать закон распределения нормальным. Помещаем вызов функции =NORMSAMP_1(B2:B9) в ячейку В10 и =NORMSAMP_1(D2:D9) — в ячейку D10. Мы видим, что закон распределения в обоих случаях можно считать нормальным и, следовательно, можно применять параметрические критерии (см. 3.1).
- Проверяем, можно ли считать дисперсии выборок одинаковыми. Для этого сначала рассчитываем дисперсии (функция =ДИСП(В2:В9) в ячейке В11 и =ДИСП(D2:D9) в ячейке D11). Затем находим расчетное (=D11/B11) и критическое (=FРАСПОБР(0,05;8-1;8-1)) значения критерия Фишера. Поскольку критическое больше расчетного, то нуль-гипотеза о равенстве дисперсий принимается (см. 3.2.1).
- Проверяем гипотезу о равенстве средних при равных дисперсиях (см. 3.2.5).
Поскольку критическое значение критерия Стьюдента больше расчетного, то средние значения равны. Следовательно, мы можем считать, что вследствие проведения рекламных мероприятий средний объем реализации увеличился на 3000 грн.
Следует иметь в виду, что на самом деле увеличение объема продаж может быть вызвано и другими причинами, случайно совпавшими по времени с рекламной кампанией. Для того чтобы убедиться, что эффект был достигнут благодаря именно рекламе, необходимо провести специальное исследование — опрос покупателей (см. 7.2.3).
7.2. Определение наличия связи между переменными
7.2.1. Дисперсионный анализ
Например, в течение недели в трех разных местах работало несколько аптечных киосков. В дальнейшем мы можем оставить только один. Необходимо определить, существует ли статистически значимое отличие между объемами реализации препаратов в киосках. Если да, мы выберем киоск с наибольшими среднесуточным объемом реализации. Если же разница объема реализации окажется статистически незначимой, то основанием для выбора киоска должны быть другие показатели. Исходные данные для анализа приведены в табл. 7.2 (подробно метод описан в 4.3.1).
Таблица 7.2
Объем реализации в трех аптечных киосках в течение недели
| Номер | День недели | ||||||
| киоска | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й |
| 1 | 820 | 800 | 780 | 790 | 810 | 830 | 600 |
| 2 | 760 | 770 | 790 | 800 | 805 | 790 | 640 |
| 3 | 780 | 780 | 810 | 790 | 775 | 760 | 610 |
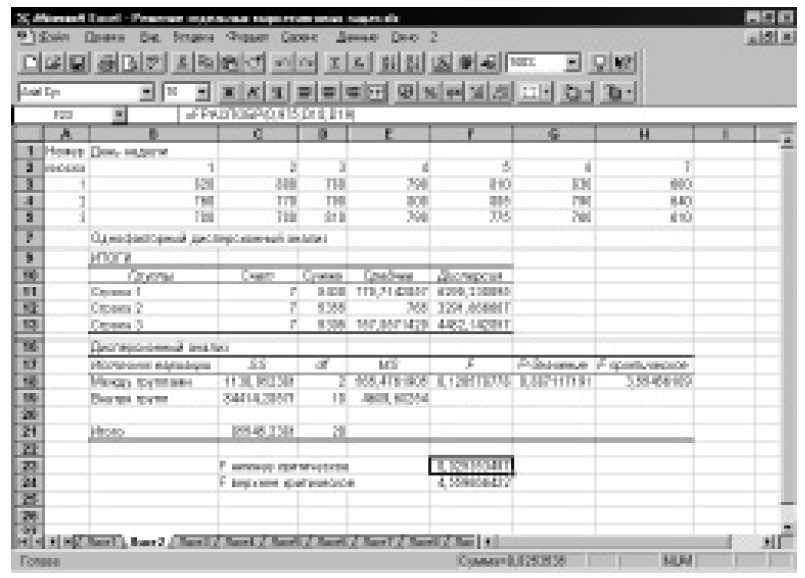
Воспользуемся однофакторным дисперсионным анализом, имеющимся в Excel. Поскольку расчетное значение критерия Фишера меньше критического, нам необходимо рассчитать новые верхнюю и нижнюю критические границы (см. Примечание к 4.3.1). Мы видим, что расчетное значение критерия Фишера (0,1205788) находится между нижней (0,0253535) и верхней (4,5596664) критическими границами (рис. 7.2). Это означает, что статистически значимого различия между внутригрупповой и межгрупповой дисперсиями не существует. То есть средний объем реализации не зависит от местоположения киоска (для данного примера).
7.2.2. Корреляционный анализ
При маркетинговых исследованиях желательно знать объемы продаж, осуществляемых фирмами-конкурентами. Эта информация обычно труднодоступна. Было бы желательно определять хотя бы приблизительно пропорции этих объемов на основании косвенных данных.
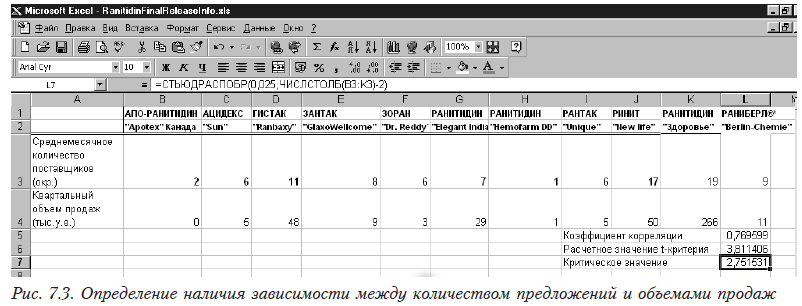
Рассмотрим[1] наличие связи между объемом продаж и активностью поставщиков аналогов ранитидина (рис. 7.3) с использованием корреляционного анализа (см. 4.2.1).
Определим коэффициент парной корреляции между этими факторами (=КОРРЕЛ(B3:L3;B4:L4)). Он равен 0,769599. Теперь проверим его значимость. Для этого рассчитаем критериальное (=L5*КОРЕНЬ(ЧИСЛСТОЛБ(B3:K3))/КОРЕНЬ(1-L5*L5)) и критическое (=СТЬЮДРАСПОБР(0,025;ЧИСЛСТОЛБ(B3:K3)-2)) значения распределения Стьюдента. Поскольку расчетное (3,811406) больше критического (2,751531), то коэффициент корреляции значим и свидетельствует о наличии статистической связи между этими двумя величинами.
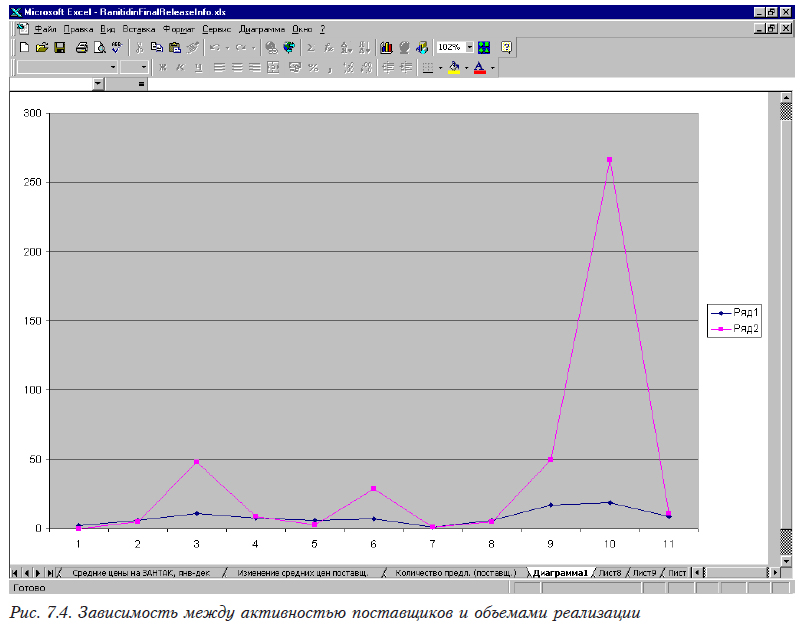
Обращаем внимание на то, что это только фиксация наличия связи, а не формула для расчета. Кроме того, следует иметь в виду — это не линейная зависимость. Если мы построим эти ломанные (рис. 7.4), то увидим, что на самом деле есть три группы препаратов (1, 2, 4, 5, 7, 8, 11 — первая; 3, 6, 9 — вторая и 10 — третья), уровни реализации в которых резко различаются.
7.2.3. Анализ таблиц сопряженности
Пример такой задачи приведен в 4.4.3. Результаты решения задачи позволяют сделать вывод, что изменения в качестве продукции зависят от поставщика и не могут быть «списаны» на случайные колебания, вызванные сложностью технологического процесса.
Рассмотрим еще один пример, теперь для четырехклеточной таблицы сопряженности. Фирма, являющаяся оптовым продавцом лекарственных препаратов, регулярно помещает свою рекламу в «Еженедельник Аптека». Ей необходимо выяснить имеется ли связь между рекламой в этом издании и покупкой аптеками предлагаемых фирмой препаратов. Исходные данные для анализа приведены в табл. 7.3.
Таблица 7.3
Количество закупок препаратов аптеками
| Название препарата | «Еженедельник Аптека» | |
| выписывает | не выписывает | |
| Препарат А | 87 | 16 |
| Препарат Б | 430 | 198 |
Подробно теория и последовательность обработки описана в 4.4.1. Результаты обработки представлены на рис. 7.5.

Поскольку расчетное значение критерия (10,93355) больше критического (3,841455), то с доверительной вероятностью 0,95 мы принимаем гипотезу о наличии связи между рекламой в «Еженедельнике Аптека» и закупками аптеками препаратов А и Б.
Не обольщайтесь кажущейся простотой и отсутствием необходимости выполнять проверку критерия c2 — «поскольку значения в первом столбце больше вторых, то связь существует». На рис. 7.6 приведен пример, где интуитивное условие выполняется, но проверка по критерию заставляет нас принять гипотезу об отсутствии связи (расчетное значение меньше критического).

7.3. Задачи прогноза
Будущее в предвидении не всегда может быть втиснуто в правила прошлого. Нити существования переплетаются в соответствии со многими неизвестными законами.
Френк Херберт “Дети Дюны”
7.3.1. Общая постановка задачи
Задача прогноза при проведении маркетинговых исследований достаточно типична. По информации, имеющейся за некоторый период, необходимо предсказать поведение системы в следующий период. Для этого может быть использован анализ временных рядов или регрессионный анализ.
О чем необходимо помнить при прогнозе
- При построении зависимостей и дальнейшем прогнозе на их основании предполагается, что совокупность факторов, действующих на исследуемую характеристику, не изменится в прогнозируемый период. То есть принятие правительством законов, изменяющих условия экономической деятельности; экономический кризис в соседней стране и т.п. изменяют условия и делают прогноз некорректным.
- Чем больше период, тем менее точен прогноз.
При исследовании временных рядов следует помнить, что во многих случаях время не является настоящей переменной, от которой зависит исследуемый процесс. На самом деле существует один или несколько факторов, зависящих от времени, но мы не можем их обнаружить или измерить.
Построение зависимости происходит в несколько этапов:
- Выделение тренда и получение его математической модели.
- Исключение тренда из данных.
- Построение математической модели сезонной составляющей для данных, в которых исключен тренд.
- Исключение сезонной составляющей из данных.
- Построение математической модели циклической составляющей для данных, в которых исключен тренд и сезонная составляющая.
- Получение итоговой модели как суммы двух моделей тренда и периодических составляющих.
Если одна из периодических составляющих отсутствует, то пункты 3 и 4 или 4 и 5 не выполняются.
Тренд получают методом одномерного регрессионного анализа. Для получения модели сначала выбирают степень аппроксимирующего полинома. Как правило, используют или линейную (первая степень) или параболическую (вторая степень) зависимость.
7.3.2. Одномерный регрессионный анализ
Одномерный регрессионный анализ используют для прогноза зависимостей, в которых не наблюдается периодичность.
Для таких случаев строится одномерная регрессия и исследуется зависимость отклика от одной переменной, которой является время. Следует отметить, что одномерная регрессия не означает, что в модели только один регрессор — в ней может быть несколько степеней для полинома или несколько членов периодической функции.
Для одномерной регрессии существуют свои особенности, которые делают построение модели в ряде случаев непростой задачей. Это связано со следующими причинами:
- переменная, по которой строится зависимость, часто не является той переменной, от которой в действительности зависит отклик;
- по этим моделям очень часто пытаются проводить предсказание дальнейшего течения процесса, что обусловливает повышенные требования к модели;
- в этих ситуациях намного чаще наблюдаются отклонения от нормальности (для многомерной регрессии, вследствие действия закона больших чисел, отклонения относительно редки);
- часто отсутствует дисперсия воспроизводимости, которая позволила бы оценить рассеивания и правильно выбрать вид уравнения.
В связи с этим можно сформулировать некоторые общие рекомендации:
- вид аппроксимирующей модели (если возможно) следует выбирать, основываясь на теоретических положениях;
- при выборе модели следует предпочесть более простую и грубую модель более сложной и точной;
- использовать непараметрическую регрессию, в которой коэффициент определяется как медиана рассчитанных коэффициентов для различных точек;
- если это возможно, часть точек нужно выделять в контрольную подвыборку, по которой проверять полученную модель.
7.3.3. Анализ временных рядов
Анализ временных рядов изучает процессы, отклики в которых измерены через равные промежутки времени. Эти отклики непосредствено или косвенно зависят от времени. Примером таких процессов может быть объем продажи препаратов, который зависит от сезонной заболеваемости. Модель обычно представляют в виде:
![]()
где tr(t) — тренд, который представляет собой плавно изменяющуюся составляющую, обычно отражащую влияние факторов, оказывающих долговременное воздействие. Например, изменение заболеваемости может иметь длительную тенденцию к снижению или повышению, являющуюся следствием общего изменения состояния экономики государства;
S(t) — сезонная составляющая, которая отражает регулярную повторяемость процессов во времени (в году, неделе, сутках и пр.). Например, изменение количества пациентов с простудными заболеваниями или цен на сельскохозяйственную продукцию в течение года, загрузка линий связи в течение суток и т.п.;
C(t) — циклическая составляющая, описывающая длительные периоды относительного спада или подъема. Например, изменение уровня заболеваемости по некоторым нозологическим единицам в зависимости от многолетних циклов солнечной активности.
Теоретически к этим составляющим добавляются так называемые интервенции, то есть резкие изменения под влиянием непредвиденных обстоятельств, например, политических кризисов, природных катастроф и т.п., которые неизбежны, но их практически нельзя определить и локализовать во времени с точки зрения возможности предвидения.
Тренд аппроксимируют обычно с использованием одномерной полиномиальной регрессии.
Для аппроксимации периодической составляющей используют регрессионную модель следующего общего вида:

Число k подбирают экспериментальным путем для обеспечения наилучшей аппроксимации. Значения t — это номера временных периодов (месяц, квартал, час, год и пр.). Для введения в формулу их преобразуют в радианную меру по формуле 2p(t-1)/n. Если анализируются годовые данные, то пересчитанные значения времени имеют вид следующего ряда 0; 2p/12; (2p/12)*2; (2p/12)*3;… (2p/12)*11. В гармоническом анализе k обозначает так называемую гармонику. Ее значение (и соответственно число членов модели) может быть от 1 до n/2. Значение n представляет собой количество временных интервалов, например, для года (при помесячном анализе) n = 12.
Значения коэффициентов a0, ai, bi рассчитываются по формулам:
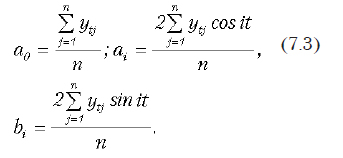
7.3.4. Примеры
Прогноз при отсутствии периодической составляющей
Наибольшую часть прогнозов представляют простые краткосрочные прогнозы, в большинстве случаев линейные. Такой прогноз выполняют следующим образом.
- Строят график зависимости изучаемой величины от времени.
- Соответственно виду графика выбирают отрезок данных, которые будут использованы для аппроксимации.
- Соответственно виду отрезка графика выбирают степень зависимости.
- Если требуемая зависимость второй степени и выше, то данные преобразовывают так, как описано в 6.6.2.
- Строят регрессионную модель.
- По полученной модели выполняют прогноз.
Например, мы имеем объемы реализации лекарственных препаратов в определенном секторе рынка (табл. 7.4).
Таблица 7.4
Объем реализации препаратов
| Период времени | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Объем реализации | 49 | 81 | 112 | 126 | 170 | 192 | 213 | 225 | 236 | 240 | 248 |
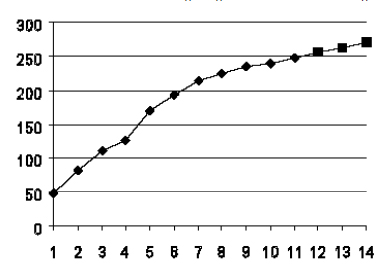
Построим по этим данным график (рис. 7.7).
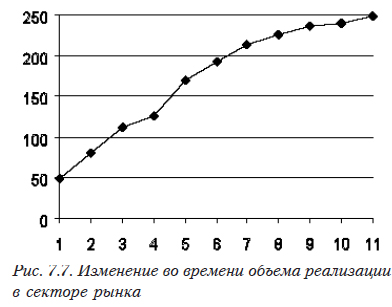
Вначале объем реализаций достаточно быстро увеличивается, затем замедляется. Кривая выглядит так, как будто сектор близок к насыщению. Для краткосрочного прогноза мы можем выбрать отрезок с 8-й по 11-ю точку и ограничиться линейной аппроксимацией.
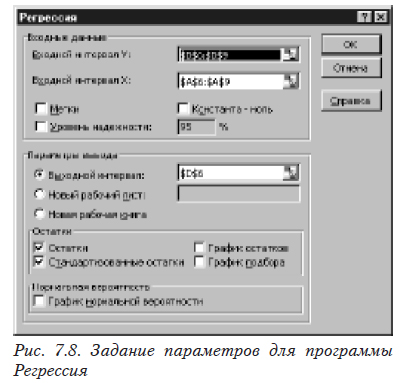
Для получения уравнения регрессии выбираем последовательно в меню «Сервис», «Анализ данных», «Регрессия». Затем заполняем задание для программы «Регрессия» (рис. 7.8). Обратите внимание, значения переменных должны располагаться в столбцах, а не в строках. В противном случае результаты расчетов программы «Регрессия» будут неправильными.
Результат работы приведен на рис. 7.9.
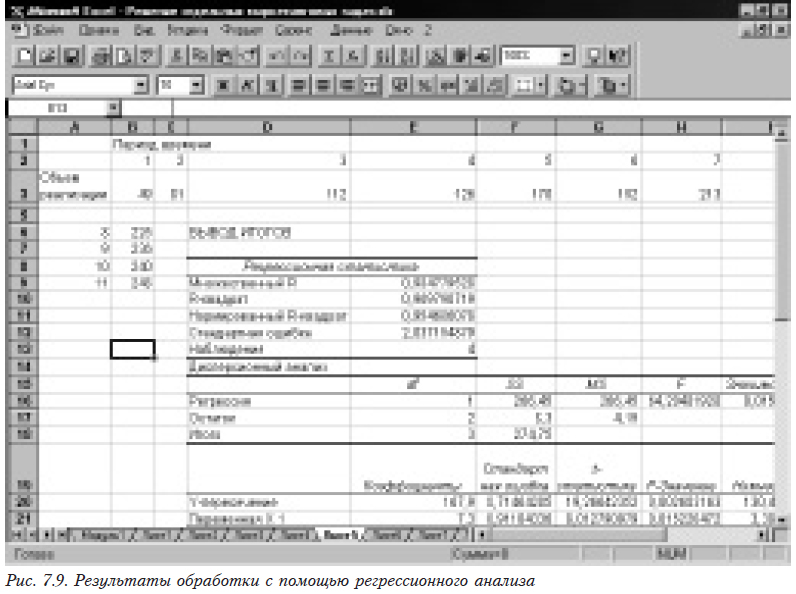
Для выполнения прогноза по полученным данным строят формулу уравнения регрессии =$E$20+$E$21*J6. Здесь J6 играет роль независимой переменной (времени).
В столбце К приведены расчетные (прогнозные) значения на следующий период времени. На рис. 7.10 представлен вид кривой, включающей и точки, значение объема реализации для которых спрогнозировано.
Прогноз при наличии периодической составляющей
Рассмотрим ситуацию, когда имеется периодическая составляющая. При торговле многими лекарственными препаратами следует отметить выраженную периодическую зависимость объема их продажи от времени года. Построение модели и прогноз в таких случаях выполняют по следующей схеме.
- Строят график зависимости изучаемой величины от времени.
- По виду графика выбирают вид тренда (линейный, параболический и пр.).
- Если предполагаемая функция тренда представляет собой зависимость второй степени и выше, то данные преобразовывают так, как описано в 6.6.2.
- Строят регрессионную модель тренда.
- Из откликов вычитаются значения, полученные по регрессионной модели.
- Для остатка строят периодическую модель (см. 7.3.3).
- Итоговую модель получают как сумму моделей, полученных в п. 4 и 6.
- По полученной модели выполняют прогноз.
В табл. 7.5 приведены данные объема реализации определенного препарата (пример базируется на реальной задаче).
Таблица 7.5
Объемы реализации
| Период времени | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Объем реализации | 137,5 | 137 | 128 | 116 | 153 | 182 | 198 |
По полученным данным строим график зависимости объема продаж от времени года. На графике можно сразу провести линию линейного тренда. Для этого в Word в меню «Диаграмма» необходимо выбрать пункт «Добавить линию тренда». Результат приведен на рис. 7.11.

Линейный тренд достаточен для описания (обычно так и бывает).
Строим регрессионную модель (см. 6). В данной ситуации, поскольку зависимость линейная, нет необходимости в преобразовании исходных данных. Результат построения модели приведен на рис. 7.12. В столбце D после этого мы рассчитываем значения объема реализации по модели. Модель имеет вид (для ячейки D3) =$C$26+$C$27*A3, на остальные ячейки столбца ее размножают перетягиванием. Здесь $C$26 и $C$27 — ссылки на коэффициенты линейной регрессионной модели, а A3 — значение соответствующего периода времени. После этого строим столбец Е, в который вводят остаток от разницы между экспериментальными значениями и значениями, рассчитанными по модели. Для этого в ячейку Е3 помещаем формулу =B3-D3, которую затем размножаем перетягиванием. Этот столбец содержит периодические изменения вокруг линии тренда (см. рис.7.12).

Теперь нам необходимо получить модель, которая будет описывать эти периодические колебания (7.3.3). Для этого сначала строим два вспомогательных столбца I и J. В I3 помещаем формулу =E3*COS(2*ПИ()*(A3-1)/$E$11), а в J3 — =E3*SIN(2*ПИ()*(A3-1)/$E$11), которые затем размножают на остальные ячейки соответствующих столбцов перетягиванием. После этого находим коэффициенты a0 (=СУММ(E3:E9)/E11), b0(=2*СУММ(I3:I9)/E11) и b1(=2*СУММ(J3:J9)/E11).
В столбце F теперь возможно рассчитать значения прогноза периодической составляющей =$C$26+$C$27*A3+$J$12+$J$13*COS(2*ПИ()*($A3-1)/$E$11)+$J$14*SIN(2*ПИ()*($A3-1)/$E$11).
Окончательная модель представляет собой сумму полученных моделей =$C$26+$C$27*(A3+7)+$J$12+$J$13*COS(2*ПИ()*($A3-6)/$E$11)+$J$14*SIN(2*ПИ()*($A3-6)/$E$11). Результаты приведены на рис. 7.13. В столбце L помещен прогноз на следующий период времени.
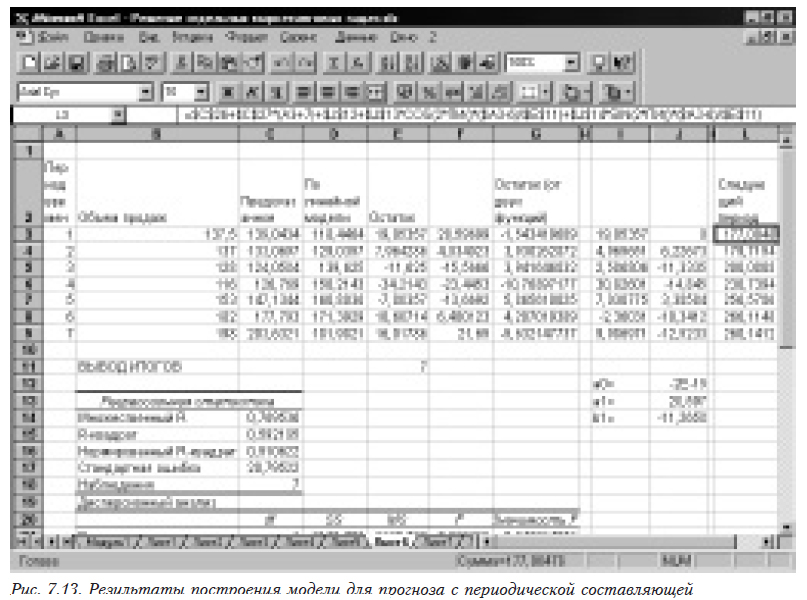
В табл. 7.6 приведены результаты расчетов по составным и окончательной моделям, а также прогноз на следующий период.
Таблица 7.6
Результаты расчетов по моделям
| Период | Эксперимент | Тренд | Сезонная составляющая | Модель | Следующий период |
| 1 | 137,5 | 118,44643 | 20,59699 | 139,0434 | 177,0048 |
| 2 | 137 | 129,03571 | 4,034023 | 133,0697 | 179,7154 |
| 3 | 128 | 139,625 | -15,5666 | 124,0584 | 200,0808 |
| 4 | 116 | 150,21429 | -23,4453 | 126,769 | 230,7394 |
| 5 | 153 | 160,80357 | -13,6692 | 147,1344 | 256,5786 |
| 6 | 182 | 171,39286 | 6,400123 | 177,793 | 266,1148 |
| 7 | 198 | 181,98214 | 21,65 | 203,6321 | 260,1412 |
На рис. 7.14 показаны графики различных составляющих моделей
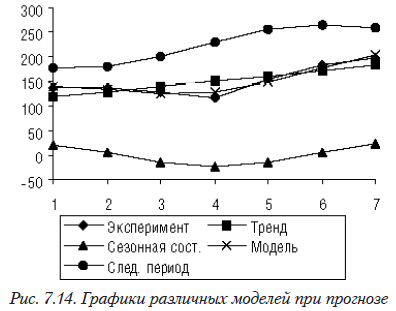
На рис. 7.15 отражены экспериментальные данные с продолжением графика по модели.
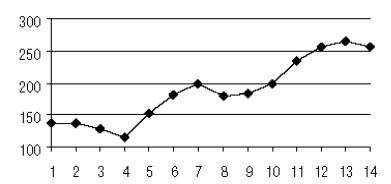
Прогнозирование при «неправильной» периодической составляющей
Рассмотрим данные относительно объема реализации препарата в оптово-розничной фирме (основано на реальной задаче) за один год полностью и часть второго года (табл. 7.7). Задача состоит в прогнозировании объемов реализации на остаток года.
Таблица 7.7
Объем продаж препарата по месяцам и годам
| Месяц года | ||||||||||||
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1998 | 125 | 150 | 120 | 110 | 101 | 90 | 103 | 165 | 196 | 165 | 151 | 123 |
| 1999 | 82 | 102 | 80 | 76 | 67 | 60 | ||||||
На рис. 7.16 представлен график, построенный по данным помесячной реализации в течение года.
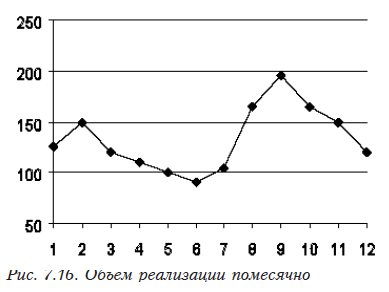
Имеется периодическая составляющая, но какая-то «неправильная». Графики, построенные для первых 6 месяцев 2 лет, отражены на рис. 7.17. Тренда как такового нет, графики практически полностью совпадают за исключением снижения объема продаж примерно на 30%.
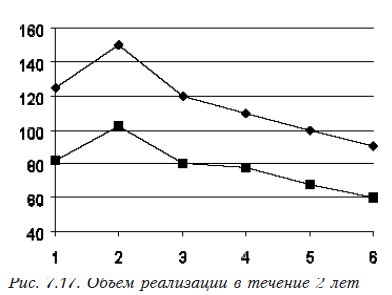
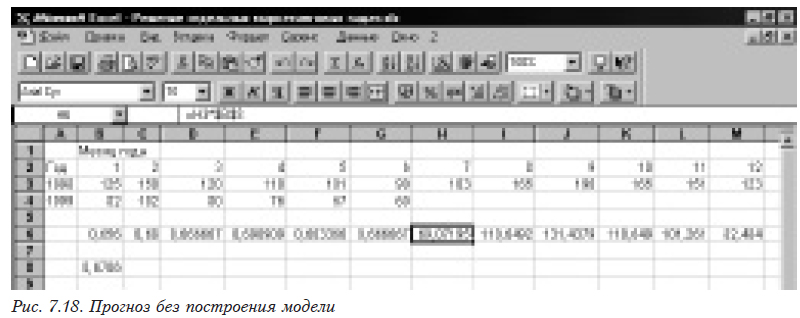
Если мы будем определять модель периодической составляющей модели, нам придется для удовлетворительной аппроксимации взять k из формулы (7.2), равное 4 или 5, что требует длительных расчетов. В такой ситуации прогноз может быть быстро выполнен без построения модели. Для этого определяем отношение объемов ежемесячных продаж одного года к таковым другого (рис.7.18). Помещаем =B4/B3 в В6, а для остальных ячеек формулу размножают перетягиванием (до G6). После этого находим среднее значение этого отношения =СУММ(B6:G6)/6. Теперь можно выполнить прогноз на остаток года. Для этого в Н6 помещаем формулу =H3*$B$8. На остальные ячейки размножают ее перетягиванием.
«Неправильная» периодическая составляющая бывает в тех ситуациях, когда эти изменения зависят в действительности не от смены времен года, а от других периодических причин. В данном примере периодическая составляющая связана с регулярными закупками товара другими оптовыми фирмами. Снижение объема реализации было связано с прекращением рекламирования препаратов, рассчитанного на розничного покупателя.
При наличии тренда в такой ситуации строится модель тренда, а затем остаток используется аналогично описанному выше для добавления периодической составляющей.
7.4. Ценовые коридоры
Задача по формированию ценовых коридоров является одной из основных в работе отдела маркетинга любой компании. Рассмотрим пример по определению ценовых коридоров для ранитидина[2] (подробное описание теории и последовательности решения см. в 3.2.10). Исходными данными являются предлагаемые цены за достаточно длительный период (полные данные есть на прилагаемой к книге дискете). По ним находят средние значения цен и внутригрупповую дисперсию (см. 3.2.10).
Для расчета внутригрупповой дисперсии воспользуйтесь приведенной ниже программой.
Option Base 1
Function in_var(indata As Object) As Double
Dim dp() As Integer
Dim Num_all As Integer
Dim i As Integer, j As Integer, k As Integer
Dim Num_groups As Integer
Dim X_aver() As Double
Dim X_vn As Double
Application.Volatile True
Num_all = indata.Rows.Count
ReDim dp(1)
ReDim X_aver(1)
Num_groups = 1
dp(Num_groups) = 0
G_tmp = indata.Cells(1, 2)
X_aver(Num_groups) = 0
For i = 1 To Num_all
dp(Num_groups) = dp(Num_groups) + 1
X_aver(Num_groups) = X_aver(Num_groups) + indata.Cells(i, 1)
If G_tmp <> indata.Cells(i, 2) Then
G_tmp = indata.Cells(i, 2)
dp(Num_groups) = dp(Num_groups) — 1
X_aver(Num_groups) = X_aver(Num_groups) — indata.Cells(i, 1)
X_aver(Num_groups) = X_aver(Num_groups) / dp(Num_groups)
Num_groups = Num_groups + 1
ReDim Preserve dp(Num_groups)
ReDim Preserve X_aver(Num_groups)
dp(Num_groups) = 1
X_aver(Num_groups) = indata.Cells(i, 1)
End If
Next i
X_vn = 0
For i = 1 To Num_groups
For j = 1 To dp(i)
k = k + 1
X_vn = X_vn + (indata.Cells(k, 1) — X_aver(i)) ^ 2
Next j
Next i
in_var = X_vn / (Num_all — Num_groups)
End Function
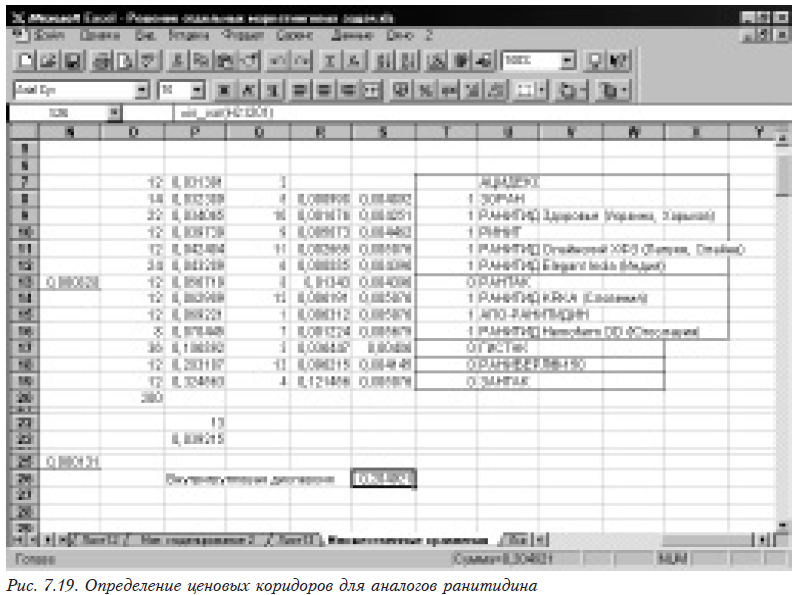
Формируем из средних значений два столбца. На рис. 7.19 в столбце N указываем количество наблюдений, по которым рассчитаны средние цены, в столбце О — непосредственно средние цены по возрастанию (в столбце Р приведены старые номера). Формируем столбец Q, в котором находится разница между соседними значениями средних цен. Для этого в ячейке Q8 помещаем формулу =O8-O7, размножаемую затем перетаскиванием на весь столбец. В столбце R помещают расчетное значение критического расстояния, вычисляемое по формуле
=СТЬЮДРАСПОБР(0,95;$N$20- $O$22)*КОРЕНЬ($O$23*($N7+$N8)/($N7*$N8)).
Если рассчитанное расстояние между средними ценами меньше критического, то они входят в один ценовой коридор. На рис. 7.19 цены, входящие в один ценовой коридор, взяты в рамку. В данном примере цены сгруппированы в пять ценовых коридоров.
7.5. Ранжирование объектов методом попарного сравнения
Задача ранжирования ряда объектов может быть как самостоятельной, так и подготовительной для задачи многокритериального выбора. В первом случае необходимо расположить объекты в порядке, соответствующем убыванию их качества или предпочтительности. Во втором располагаются не объекты, а показатели, описывающие объект, в порядке убывания их значимости.
Поскольку задача определения весов значимости при большом количестве параметров является сложной и сильно влияющей на результаты оценок рейтинга, используют процедуру, позволяющую повысить точность определения весов. Для этого эксперт попарно сравнивает два параметра и оценивает их значимость относительно друг друга. Задача попарного сравнения гораздо проще, чем составление всех весов и, благодаря большому количеству градаций, достаточно точная (табл. 7.7). По результатам всех ответов выполняют расчет весов. Эксперт оценивает также показатели, которые не имеют определенного установленного значения.
Таблица 7.7
Градации сравнения критериев по их значимости для достижения конечной цели
| Название первого критерия | Градация | Название второго критерия |
| А | Эквивалентный | В |
| А | Важнее | В |
| А | Значительно важнее | В |
| А | Существенно важнее | В |
| А | Безусловно важнее | В |
| В | Важнее | А |
| В | Значительно важнее | А |
| В | Существенно важнее | А |
| В | Безусловно важнее | А |
Для примера рассмотрим сравнение с меньшим количеством градации сравнения (табл.7.8). Такая система проще для эксперта.
Таблица 7.8
Трехуровневая система градации сравнения
| Название первого критерия | Градация | Название второго критерия |
| А | Эквивалентны | В |
| А | Важнее | В |
| В | Важнее | А |
Для выполнения сравнения необходима дополнительная таблица 7.9.
Таблица 7.9
Баллы, добавляемые при сравнении
| Градация | Критерий А | Критерий В |
| Эквивалентны | 0,5 | 0,5 |
| А Важнее В | 1 | 0 |
| В Важнее А | 0 | 1 |
При сравнении показателей часто возникает психологическая проблема: как сравнивать казалось бы несравнимые вещи. Ответ состоит в том, что критерии сравнивают с точки зрения их важности для качества объекта при выбранном способе его использования. В каждом конкретном случае сравнения значимость критериев будет различна. Так, при необходимости спасения жизни больного на первом месте будет эффективность действия препарата, а не его цена. При хроническом заболевании в ряде случаев цена может быть важнее (при сравнении препаратов-аналогов).
Пример
Рассмотрим пример ранжирования критериев для сравнения препаратов.
При заполнении табл. 7.10 выполняем сравнение в направлении, указанном стрелкой по строкам (таблица не симметрична!). На основании табл. 7.9 по результатам сравнения заполняем соответствующие ячейки (заполнено по ответам специалистов ИфиТ АМН). Если «Формы» менее важны чем «Спецактивность», то в соответствующей ячейке записывают 0. При равной важности «Форм» и «Сырьевой базы» в соответствующую ячейку заносят 0,5. Если «Спецактивность» важнее «Противопоказаний», то в соответствующую ячейку заносят 1.
Таблица 7.10
Сравнение значимости критериев
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| ð | Формы | Спецактивность | Сырьевая база | Противопоказания «средние» | Противопоказания «тяжелые» | Дополнительные полезные свойства | Сумма | Веса |
| Формы | 0 | 0,5 | 0 | 0 | 0 | 0,5 | 0,034 | |
| Спецактивность | 1 | 1 | 1 | 1 | 1 | 5 | 0,34 | |
| Сырьевая база | 0,5 | 0 | 0 | 0 | 0 | 0,5 | 0,034 | |
| Противопоказания «средние» | 1 | 0,5 | 1 | 0 | 0,5 | 3 | 0,207 | |
| Противопоказания «тяжелые» | 1 | 0 | 1 | 1 | 1 | 4 | 0,276 | |
| Дополнительные полезные свойства | 1 | 0 | 0,5 | 0 | 0 | 1,5 | 0,103 |
В столбец «Сумма» заносят суммы по строке. Этот столбец и может служить в качестве рейтинга критериев. Диаграмма этого рейтинга приведена на рис. 7.20.

7.6. Многокритериальный выбор
Lulla lex satis commodo omnibus est[3].
Liv., Hist., XXXIV, 3
Приобретая корову, вы одновременно приобретаете и ее рога.
Пословица о. Маврикий
При решении реальных задач объект обычно характеризуется не одним, а несколькими показателями функционирования (откликами). При оптимизации требования к ним могут быть достаточно противоречивыми, то есть, улучшая один показатель, мы неминуемо ухудшаем часть остальных. Поэтому возникает задача определения некоторой компромиссной точки, в равной степени удовлетворяющей всем требованиям (компромисс по Парето). Как правило, результаты по каждому отдельному показателю качества будут хуже, чем в случае однокритериальной оптимизации по этому параметру. Каждому препарату соответствует точка в многомерном пространстве, координатами которой являются параметры, описывающие препарат. Пространство нормировано в единичный гиперкуб таким образом, что по каждой координате движение от 0 к 1 соответствует изменению параметра от наихудшего значения к наилучшему. Тогда точка с координатами {1, 1, 1, …1} всегда соответствует гипотетическому объекту, который имеет наилучшие из возможных значений по всем параметрам. Расстояние от этой вершины гиперкуба к точке, соответствующей положению конкретного объекта, соответствует удаленности объекта от наилучшего значения и представляет величину, обратную рейтингу объекта. Таким образом, мы получаем строгую, формализованную и имеющую простую геометрическую интерпретацию процедуру построения ранжированного ряда (определения рейтинга). В случае неравнозначности различных параметров для определения рейтинга объектов, при вычислении расстояний в формулу вычисления расстояний достаточно добавить веса, соответствующие значимости параметров (см. 7.5).
Таблица 7.11
Возможные цели, задаваемые по каждому критерию
| Цель | Уточнение цели |
| Без ограничений | |
| Минимум | + Ограничение Уi > a |
| + Ограничение Уi і a | |
| Без ограничений | |
| Максимум | + Ограничение Уi < a |
| + Ограничение Уi Ј a | |
| Интервал | В центр |
| В произвольное место | |
| Уi > a | |
| Полуинтервал | Уi і a |
| Уi < a | |
| Уi Ј a | |
| Константа | а |
| Игнорировать | — |
Фактически, часть этих целей является ограничениями.
В предлагаемой программе используются только два вида целей: минимум и максимум, что достаточно для подавляющего большинства задач, поскольку остальные можно свести при формализации задачи к этим двум.
Программа
Для получения рейтинга объектов по их характеристикам используется следующая программа:
Option Base 1
Sub OptObjCh()
‘Подпрограмма выбора оптимального объекта
‘из имеющейся совокупности данных
‘Ввод ссылки на область с указанием целей
Set tagCELL = Application.InputBox( _
prompt:=»Выберите область целей и их ограничений», _
Type:=8)
num_col_tag = tagCELL.Columns.Count
‘Ввод ссылки на область с коэффициентами важности
Set waightCELL = Application.InputBox( _
prompt:=»Выберите коэффициенты важности», _
Type:=8)
‘Формирование рабочего массива весовых коэффициентов
ReDim w(1 To num_col_tag)
W_sum = Application.Sum(waightCELL)
For i = 1 To num_col_tag
w(i) = waightCELL.Cells(i) / W_sum
Next i
‘Ввод ссылки на наименования критериев качества
Set nameCELL = Application.InputBox( _
prompt:=»Выберите массив названий критериев качества», _
Type:=8)
Set nameobjCELL = Application.InputBox( _
prompt:=»Выберите массив названий объектов», _
Type:=8)
‘Ввод ссылки на матрицу данных
Set matdataCELL = Application.InputBox( _
prompt:=»Выберите массив данных (без заголовков)», _
Type:=8)
‘Поиск максимального и минимального значений для каждого критерия качества
Row_data = matdataCELL.Rows.Count ‘Вычисление количества строк
Col_data = matdataCELL.Columns.Count ‘Вычисление количества столбцов
If Col_data <> num_col_tag Then
MsgBox «Ошибка в данных»: GoTo en
End If
ReDim Ymax(1 To Col_data)
ReDim Ymin(1 To Col_data)
For i = 1 To Col_data
Ymin(i) = Application.Min(matdataCELL.Columns(i))
Ymax(i) = Application.Max(matdataCELL.Columns(i))
Next i
‘Ввод ссылки на ячейку с которой будут выводится результаты
Set myCell3 = Application.InputBox( _
prompt:=»Выберите ячейку, с которой будут выводится результаты», _
Type:=8)
ReDim dob(1 To Col_data)
ReDim Ycarent(1 To Col_data)
ReDim Yobcarent(1 To Row_data)
ReDim dotsnum(1 To Row_data)
For K = 1 To Row_data
Yobcarent(K) = 0
dotsnum(K) = K
For i = 1 To Col_data
If tagCELL.Cells(i) = «min» Then
dob(i) = (1 + (Ymin(i) — matdataCELL.Cells(K, i)) / (Ymax(i) — Ymin(i)))
ElseIf tagCELL.Cells(i) = «max» Then
dob(i) = (1 — (Ymax(i) — matdataCELL.Cells(K, i)) / (Ymax(i) — Ymin(i)))
Else
MsgBox «Ошибка в данных»: GoTo en
End If
Yobcarent(K) = Yobcarent(K) + (1 — dob(i)) * (1 — dob(i)) * w(i)
Next i
Yobcarent(K) = Sqr(Yobcarent(K))
Next K
For i = 1 To Row_data
Yobcarent(i) = 1 — Yobcarent(i)
Next i
‘Сортировка массива обобщенных критериев
Counter = 1 ‘ Инициализация индикатора перестановок.
While Counter = 1 ‘ Анализ значения индикатора перестановок.
Counter = 0
For i = 1 To Row_data — 1
If Yobcarent(i) < Yobcarent(i + 1) Then
tp = Yobcarent(i)
t_dot = dotsnum(i)
Yobcarent(i) = Yobcarent(i + 1)
dotsnum(i) = dotsnum(i + 1)
Yobcarent(i + 1) = tp
dotsnum(i + 1) = t_dot
Counter = 1
End If
Next i
Wend
myCell3.Offset(0, 0).Value = _
«Результаты поиска оптимального объекта»
‘ Вывод параметров наилучшего объекта
myCell3.Offset(1, 0).Value = «Критерии»
myCell3.Offset(1, 0).Borders.Item(xlBottom).LineStyle = xlContinuous
For i = 1 To Col_data
myCell3.Offset(1, i).Value = nameCELL.Cells(i)
myCell3.Offset(1, i).Borders.Item(xlBottom).LineStyle = xlContinuous
Next i
myCell3.Offset(2, 0).Value = «Цели»
myCell3.Offset(2, 0).Borders.Item(xlBottom).LineStyle = xlContinuous
For i = 1 To Col_data
myCell3.Offset(2, i).Value = tagCELL.Cells(i)
myCell3.Offset(2, i).Borders.Item(xlBottom).LineStyle = xlContinuous
Next i
myCell3.Offset(3, 0).Value = «Веса»
myCell3.Offset(3, 0).Borders.Item(xlBottom).LineStyle = xlDouble
For i = 1 To Col_data
myCell3.Offset(3, i).Value = w(i)
myCell3.Offset(3, i).Borders.Item(xlBottom).LineStyle = xlDouble
Next i
myCell3.Offset(5, 0).Value = «Объекты»
myCell3.Offset(5, 1).Value = «Эффективность»
myCell3.Offset(5, 1).Columns.AutoFit
myCell3.Offset(5, 0).Borders.Item(xlBottom).LineStyle = xlDouble
myCell3.Offset(5, 1).Borders.Item(xlBottom).LineStyle = xlDouble
myCell3.Offset(5, 0).Borders.Item(xlRight).LineStyle = xlDouble
For K = 1 To Row_data
myCell3.Offset(5 + K, 0).Value = nameobjCELL.Cells(dotsnum(K))
myCell3.Offset(5 + K, 0).Borders.Item(xlRight).LineStyle = xlDouble
myCell3.Offset(5 + K, 0).Borders.Item(xlBottom).LineStyle = xlContinuous
‘ For i = 1 To Col_data
‘ myCell3.Offset(5 + K, i).Value = matdataCELL.Cells(dotsnum(K), i)
‘Next i
myCell3.Offset(5 + K, 1).Value = Yobcarent(K)
myCell3.Offset(5 + K, 1).Borders.Item(xlBottom).LineStyle = xlContinuous
Next K
en:
End Sub
Пример
Проведем сравнение лекарственного средства амизон, предложенного Институтом фармакологии и токсикологии АМН, с другими ненаркотическими анальгетиками: аспирином, анальгином, диклофенаком, индометацином, ибупрофеном, пироксикамом. Экспериментальные данные получены в отделе чл.-кор. АМН Ф.П. Тринуса д-ром мед. наук Т.А.Бухтияровой.
В качестве критериев сравнения были использованы: анальгезирующая активность (в тесте «корчи» и по методу «горячая пластинка»), противовоспалительная активность, основные фармакокинетические параметры, противопоказания и побочные эффекты, а также показания к применению (табл. 7.12).
Таблица 7.12
Таблица несовпадающих характеристик препаратов
| Анальгезирующая активность | Противовоспалительная активность | Заболевания | Противопоказания | Побочные эффекты | ||||||||||||||
| Препарат | Корчи | Горячая пластинка | ||||||||||||||||
| ЕД50 | ТИ | ЕД50 | ТИ | ЕД50 | ТИ | |||||||||||||
| Амизон | 14 | 159 | 24 | 93 | 10 | 223 | 5 | 2 | 1 | |||||||||
| Аспирин | 155 | 10 | 480 | 3 | 98 | 16 | 4 | 3 | 6 | |||||||||
| Анальгин | 55 | 60 | 93 | 35 | 90 | 90 | 5 | 4 | 3 | |||||||||
| Диклофенак | 5 | 74 | 98 | 3,78 | 8 | 46,25 | 4 | 6 | 6 | |||||||||
| Индометацин | 11 | 4,27 | 40 | 1,18 | 10 | 4,7 | 4 | 6 | 9 | |||||||||
| Ибупрофен | 170 | 4,41 | 370 | 2,0 | 48 | 15,63 | 4 | 6 | 8 | |||||||||
| Кетопрофен | 180 | 5,11 | 550 | 1,67 | 33 | 27,88 | 2 | 3 | 7 | |||||||||
| Напроксен | 63 | 9,84 | 310 | 2 | 15 | 41,33 | 4 | 6 | 7 | |||||||||
| Пироксикам | 92 | 3,15 | 145 | 2 | 20 | 14,5 | 4 | 6 | 7 | |||||||||
На первом этапе способом, изложенным в 7.5, была определена значимость критериев (рис. 7.21). Следует иметь в виду, что разные эксперты в зависимости от цели сравнения могут формировать разные списки критериев и их значимость.
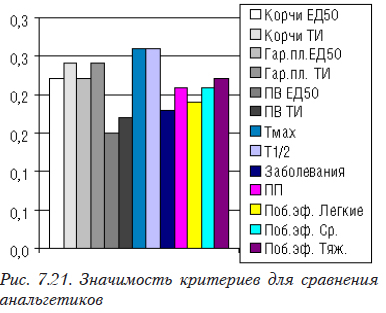
Сначала формируем исходные данные (рис. 7.22). При этом в строке «Цели» записываем, какое значение данного критерия является наилучшим: минимальное (min) или максимальное (max). В строке «Веса» помещаются значения весовых коффициентов, вычисленные ранее.
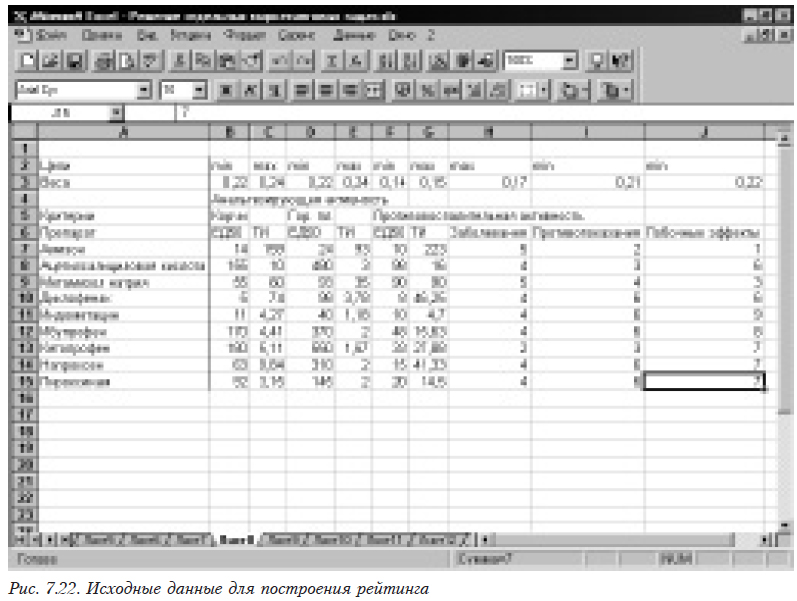
После этого в меню последовательно выбираем пункты «Сервис», «Макрос» (для Excel-97 и выше еще и «Макросы»). В появившемся окне выбираем макрос OptObjCh. Затем в последовательно появляющихся окнах вводим ссылки на необходимые для программы данные: сначала — на строку, в которой указаны цели по критериям (рис. 7.23).
Затем необходимо ввести строку, содержащую веса (рис.7.24).

Затем вводится ссылка на названия критериев (рис. 7.25).

В следующем окне вводят ссылку на названия объектов (рис. 7.26).
Затем вы вводите ссылку на массив исходных данных, исключая названия объектов и критериев (рис. 7.27).
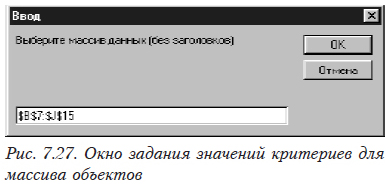
Последней вводят ссылку на ячейку, начиная с которой (вправо и вниз) будут размещаться результаты (рис. 7.28).

Результаты работы программы приведены на рис. 7.29. Обратите внимание, что список объектов расположен в порядке убывания рассчитанного рейтинга.

Диаграмма рейтингов объектов приведена на рис. 7.30.
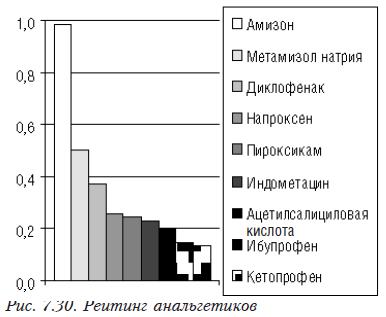
Диаграмма позволяет легко сравнить все препараты. По оси У указано относительное значение рейтинга (от 0 до 1). Значение 1 отвечает гипотетическому объекту с наилучшими значениями по всем показателям.
Таким образом, предложенный подход позволяет корректно проводить сравнения препаратов при наличии большого количества характеризующих их показателей и неравнозначности этих показателей для результатов сравнения.
7.7. Статистические методы контроля качества
7.7.1. Контрольные карты [4]
Контрольные карты были разработаны в Bеll Telephone Laboratories (США) в 1924 г. для отделения вариаций, вызванных определенными причинами, от случайных вариаций.
Для любого технологического процесса неизбежны ситуации, когда он постепенно выходит из-под контроля: вследствие износа оборудования, воздействия колебаний температуры, изменения влажности, вариации свойств сырья и вспомогательных материалов, энергопитания и т.д. Чтобы не допустить появления бракованной продукции, необходимо отслеживать начинающиеся изменения и прогнозировать их последствия.
Общий вид контрольной карты изображен на рис. 7.31.
Центральная линия соответствует среднему значению. Внутренние контрольные границы проводятся в , а внешним контрольным границам соответствует , где s — среднеквадратическое отклонение. При этом внутренние границы соответствуют доверительной вероятности 0,95; а внешние — 0,997. Это означает, что для контролируемого (налаженного) технологического процесса внутри внешних контрольных границ должно находиться 99,7% контролируемых значений, а внутри внутренних контрольных границ — 95%.
На картах регулярно отмечаются измеряемые значения контролируемых параметров технологического процесса. Признаками выхода технологического процесса из-под контроля являются следующие ситуации:
- за внешние пределы попадает более трех точек из 1000;
- между внутренними и внешними границами находится более одной точки из 20;
- по одну сторону центральной линии находится 10 точек из 11, 12 из 14 или 16 из 20 (взятых подряд);
- наличие тренда (рис. 7.32);
- наличие периодичности (рис. 7.33).
Возникновение вышеуказанных ситуаций требует остановки технологического процесса и его переналадки или устранения причин их вызвавших.

Если обнаружено, что все точки находятся внутри интервала , это означает, что вы неправильно выбрали контрольные границы.


Дискретные карты
Иногда возникают ситуации, когда отсутствуют параметры, измерение которых позволяет составить представление о происходящих в технологическом процессе изменениях. Мы можем судить о них только по доле бракованных изделий. В таких случаях применяют дискретные карты (они имеют такой же внешний вид, как и контрольные). Контрольные границы для них определяют следующим образом. При налаженном технологическом процессе выбирается такой объем выборки n, чтобы в нее попадало 1–5 бракованных изделий. Собираются данные для 20–25 таких групп. Затем определяют . Здесь k — число выборок, n — объем выборки, а Li — количество бракованных изделий в конкретной выборке. Затем определяют верхние и нижние контрольные границы . Если расчетная нижняя граница оказывается отрицательной, ее принимают равной нулю.
Карты сумм
Недостаток контрольных карт в том, что они позволяют обнаружить уже свершившийся факт — выход технологического процесса из-под контроля. Однако желательно предупреждать подобные ситуации, то есть необходимо увидеть заранее тенденции, которые могут привести к нарушениям технологического процесса. Для этого используют карты сумм. На них откладывают накапливаемые отклонения от среднего — из каждого полученного значения вычитают среднее, а затем суммируют со всеми ранее полученными отклонениями, а результат откладывают на карте. Если процесс находится под контролем, то накапливаемые суммы должны колебаться вокруг нулевой линии. Когда же наблюдают какие-либо тенденции, это свидетельствует о наличии причин, вызывающих отклонение от нормального течения технологического процесса (рис. 7.34).
Накапливаемая сумма отклонений

7.7.3. Диаграммы причин и результатов
Диаграммы, отражающие причины и результаты, называют также «рыбий скелет», «дерево», «речные притоки», диаграмма Исикавы (рис. 7.35). Их широко используют при формализации задачи для систематизации списка причин или определения причин, влияющих на определенный показатель качества.
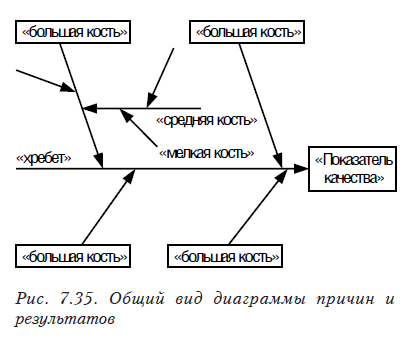
Использование диаграмм позволяет обнаружить элементы, которые необходимо проверить, устранить, модифицировать или добавить. При анализе следует акцентировать внимание на том, как сильно изменение исследуемого фактора влияет на показатель качества.
Построение диаграмм для определения причин выполняют следующим образом:
- определяют показатель качества;
- выбирают основные причины («большие кости»);
- определяют вторичные причины («средние кости»), влияющие на основные, а затем третичные («мелкие кости»), влияющие на вторичные;
- выполняют ранжирование факторов по их значимости и выделяют особо значимые.
Построение диаграмм для систематизации списка причин выполняют следующим образом:
- выбирают показатель качества;
- отыскивают как можно больше причин, которые, возможно, влияют на этот показатель;
- устанавливают отношения между причинами вида «причина — результат» и составляют диаграмму. При этом лучше рассматривать последовательность причин от «мелких костей» к средним и от средних к крупным;
- выполняют ранжировку факторов для выделения наиболее важных из них.
Для ранжирования факторов можно воспользоваться экспертными оценками и методом попарного сравнения (см. 7.6).
7.8. Анализ экспертных оценок
При маркетинговых исследованиях часть информации представляет собой экспертные оценки, которые перед использованием необходимо проанализировать на согласованность. Для решения общей задачи согласованности применяют методы ранговой корреляции и конкордации (см. 4.2.3). Здесь же мы рассмотрим действия по анализу экспертных оценок в случаях несогласованности мнений. Действия, описанные ниже, выполняют, когда экспертов достаточно много (во всяком случае, больше двух).
Если мнения экспертов несогласованны, можно выбрать один из вариантов действий:
- удалить эксперта, мнение которого расходится с мнением остальных;
- удалить объект, вызывающий разногласия;
- распределить экспертов на группы по согласованности мнений, а анализ производить отдельно по каждой группе.
Вариант выбирают в зависимости от условий решаемой задачи. Для отработки данных вариантов анализа разработаны эвристические алгоритмы.
Удаление эксперта
- Рассчитать для всех экспертов матрицу ранговых коэффициентов корреляции Спирмена.
- Найти эксперта, для которого r(k, i) — min « i О 1,… m, то есть мнение этого эксперта менее всего согласуется с мнением остальным. Отсутствие такового означает, что, возможно, мы имеем дело с разделением мнений экспертов на несколько групп.
- В случае неудачи по действиям в п. 2, можно попытаться найти эксперта, для которого среднее значение r(k, i) минимально.
- Выполнить проверку согласованности экспертов после удаления выбранного. Если мнения остаются несогласованными, это означает, что выбран не тот путь.
Удаление объекта, вызывающего разногласия экспертов
- Выбрать объект, для которого дисперсия рангов будет максимальной, то есть:
— — min,
где Xij — ранг присвоенный i-му объекту j-м экспертом, Xi — средний ранг для i-го объекта, m — количество экспертов. Больше всего разногласий вызывает объект с максимальной дисперсией рангов.
- Выполнить проверку согласованности экспертов после удаления выбранного объекта.
Распределение экспертов на группы, в которых мнение согласованно
Для этого можно использовать метод кластерного анализа, приняв за расстояние между экспертами величину abs(r(k,i)), то есть чем больше согласованность между экспертами, тем меньше расстояние между ними (см. 5.1).
Пример
Рассматривая эти специально созданные примеры, не надейтесь, что в реальной жизни возможно выполнить перечисленные операции без расчетов. Во многих случаях «здравый смысл» и точный расчет не совпадают (например, рис. 7.5 и 7.6). Кроме того, в ряде случаев результаты маркетингового исследования представляются другой стороне (руководству, заказчику), для которых необходимо, чтобы выводы были доказаны.
Для расширения производства или увеличения продаж из множества потенциально выгодных препаратов необходимо выбрать один. Времени и денег для проведения тщательных маркетинговых исследований нет. Поэтому для определения препарата мы выбираем экспертов, которые будут оценивать каждый препарат по 100-балльной шкале. При этом в число экспертов должны войти представители различных специальностей — они не должны быть представителями одного предприятия и одной специальности (например, маркетологами). Оценки экспертов должны быть независимыми (табл. 7.13).
Таблица 7.13
Пример задачи для удаления эксперта
| Эксперты | |||||
| Препараты | А | Б | В | Г | Д |
| 1 | 91 | 97 | 70 | 93 | 88 |
| 2 | 92 | 90 | 65 | 90 | 87 |
| 3 | 80 | 83 | 85 | 81 | 79 |
| 4 | 74 | 70 | 40 | 76 | 69 |
| 5 | 95 | 99 | 67 | 100 | 92 |
| 6 | 67 | 60 | 95 | 70 | 57 |
| 7 | 32 | 43 | 20 | 30 | 25 |
| 8 | 45 | 50 | 82 | 51 | 41 |
| 9 | 46 | 50 | 30 | 52 | 44 |
| 10 | 99 | 95 | 71 | 100 | 93 |
Находим коэффициент конкордации (см. в 4.2.3). Значение 0,740261 не является достаточно большим (рис. 7.36), полученное число должно быть близким к 0,9.
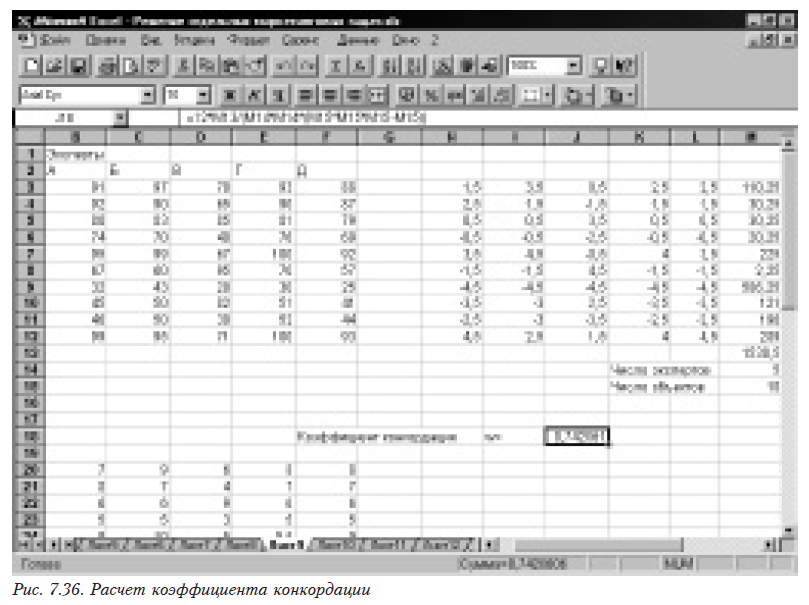
Проведем операции для выявления выделяющегося эксперта. Для этого сначала построим матрицу рангов. Помещаем в В20 формулу =Rank1(C3;C$3:C$12;1), а затем размножаем ее перетягиванием на ячейки от В29 до F29. Затем для каждого столбца, соответствующего мнению одного эксперта, необходимо найти суммы квадратов разностей рангов между этим столбцом и всеми остальными. Например, для второго столбца, помещаем формулу =(B20-$C20)*(B20-$C20) в ячейку G31, а затем размножаем ее перетягиванием на ячейки от G31 до К39. После этого в ячейку К41 помещаем формулу =СУММ(G31:K39). Аналогично выполняем расчеты для остальных экспертов (см. рис.7.37).
Рассчитывать сами коэффициенты корреляции рангов нет необходимости, поскольку они изменяются пропорционально рассчитанным суммам квадратов разницы рангов. Мы видим, что это значение для третьего эксперта (475,75) резко отличается от аналогичных значений для других экспертов (129,76; 133,25; 132,5; 133).
Мы выявили эксперта, мнение которого отлично от мнения остальных. Возникает вопрос, чьим мнением воспользоваться: группы согласных друг с другом или эксперта с особым мнением? Ведь мнение большинства не всегда отражает истину.
Таблица 7.14
Пример задачи для удаления спорного объекта
| Эксперты | |||
| Препараты | А | Б | В |
| 1 | 32 | 29 | 34 |
| 2 | 80 | 85 | 78 |
| 3 | 61 | 65 | 63 |
| 4 | 81 | 32 | 95 |
| 5 | 91 | 90 | 93 |
| 6 | 62 | 67 | 59 |
| 7 | 50 | 50 | 55 |
| 8 | 42 | 45 | 44 |
| 9 | 69 | 71 | 67 |
| 10 | 100 | 99 | 98 |
Полученный коэффициент конкордации не очень большой (0,859933). Построим матрицу рангов (см. предыдущий пример) и для каждой строчки найдем дисперсию, задав вызов функции =ДИСП(B20:D20) в ячейке F20, затем размножив ее перетягиванием на остальные строки (рис. 7.38).

Мы видим, что наибольшую, резко выделяющуюся дисперсию имеет объект «Препарат 4».
Если это непринципиально, то спорный объект удаляется из группы рассматриваемых объектов. Желательно также выяснить причину противоречивого мнения экспертов. Наиболее частыми причинами противоречия мнений экспертов могут быть:
- отсутствие или недостаточность информации об объекте;
- принадлежность экспертов к разным научным школам;
- противоречивая информация об объекте.
После удаления спорного объекта коэффициент конкордации повысился до 0,97348.
Таблица 7.15
Пример для разделения экспертов на независимые группы
| Эксперты | ||||||||
| Препараты | А | Б | В | Г | Д | Е | Ж | З |
| 1 | 98 | 100 | 99 | 40 | 40 | 48 | 69 | 72 |
| 2 | 65 | 66 | 61 | 67 | 70 | 66 | 30 | 34 |
| 3 | 32 | 28 | 29 | 92 | 94 | 91 | 81 | 86 |
| 4 | 53 | 57 | 55 | 50 | 51 | 50 | 94 | 95 |
| 5 | 27 | 25 | 23 | 84 | 85 | 83 | 64 | 65 |
| 6 | 100 | 99 | 100 | 50 | 52 | 54 | 72 | 76 |
| 7 | 48 | 50 | 51 | 44 | 46 | 43 | 32 | 34 |
| 8 | 23 | 22 | 24 | 81 | 82 | 79 | 80 | 82 |
| 9 | 99 | 97 | 99 | 47 | 45 | 49 | 50 | 52 |
| 10 | 63 | 64 | 62 | 32 | 35 | 31 | 45 | 51 |
Рассчитываем коэффициент конкордации (рис. 7.39). Его величина (0,38475) мала.

Проведем распределение экспертов на группы. Сначала строим матрицу рангов, затем — матрицу корреляционных коэффициентов Кендалла для всех сочетаний пар экспертов. Для этого помещаем требуемые формулы в указанные ячейки (табл.7.16), а затем размножаем их перетягиванием на остаток строки.
Таблица 7.16
Формулы расчета коэффициентов корреляции
| Ячейка | Формула |
| В28 | =1-4*Candall_K($B$15:$B$24;C$15:C$24)/( $S$15*($S$15-1)) |
| C29 | =1-4*Candall_K($C$15:$C$24;D$15:D$24)/( $S$15*($S$15-1)) |
| D30 | =1-4*Candall_K($D$15:$D$24;E$15:E$24)/( $S$15*($S$15-1)) |
| E31 | =1-4*Candall_K($E$15:$E$24;F$15:F$24)/( $S$15*($S$15-1)) |
| F32 | =1-4*Candall_K($F$15:$F$24;G$15:G$24)/( $S$15*($S$15-1)) |
| G33 | =1-4*Candall_K($G$15:$G$24;H$15:H$24)/( $S$15*($S$15-1)) |
| H34 | =1-4*Candall_K($H$15:$H$24;I$15:I$24)/( $S$15*($S$15-1)) |
Получив коэффициенты корреляции (рис.7.40), проанализируем их. Имеются три отчетливо выраженные группы экспертов, коэффициенты корреляции между членами этих групп выше 0,9, в то время как коэффициенты корреляции с другими экспертами — меньше 0,4. В первую группу входят эксперты А, Б и В, во вторую — Г, Д, Е, а в третью Ж и З.

После распределения экспертов на группы необходимо определить, мнение какой группы положить в основу принимаемого решения. Обязательно следует проверить составы групп экспертов — может оказаться, что, например, в одной группе — только маркетологи, в другой — оптовые продавцы и др.
Выбирается тот препарат, среднее значение оценок по которому будет наибольшим.
7.9. Разработка методов оценки объема рынка для лекарственного средства
Одной из важных задач при выполнении маркетинговых исследований является оценка сектора рынка конкретного лекарственного средства. В данной работе предлагается подход, который, по мнению авторов, позволяет определить объем сектора с большей обоснованностью, чем при традиционных способах определения[5].
Опорной величиной для определения объема рынка лекарственного средства является потребность в нем, обусловленная заболеваемостью.
Следующий шаг — определение максимального объема рынка, то есть возможного объема при отсутствии конкурентов. Определяется покупательной способностью населения и мотивационными побуждениями — важность его приобретения с точки зрения индивидуума (для кого, зачем, при каких обстоятельствах). При расчетах исходили из следующих предположений:
- распространенность заболеваемости среди различных категорий населения одинакова, независимо от уровня доходов (исключения следует делать только для отдельных заболеваний);
- структура населения по доходам близка к таковой: 10% — состоятельные, 80% — бедные, 10% — с доходами ниже прожиточного уровня. При этом для представителей первой и третьей групп цена не имеет значения (только одни будут покупать, невзирая на цену, а другие не будут покупать ни при каких обстоятельствах).
Для большинства населения вопрос приобретения лекарственных препаратов зависит от силы мотивации в конкретном случае. Вопрос покупки в процессе решения индивидуумом состоит из трех частей:
- покупать или не покупать вообще;
- решение о цене, которую он готов заплатить;
- выбор конкретного лекарственного средства.
На каждый из этих этапов воздействуют различные факторы. Так, вероятность приобретения лекарственного средства повышается, если:
- болен ребенок;
- отсутствие лечения представляет опасность для жизни, трудоспособности, внешнего вида больного;
- на препарат выписан рецепт или он рекомендован врачом при визите к нему;
- непринятие лекарственного средства создает постоянные неудобства в повседневной жизни, снижает трудоспособность, ухудшает внешний вид и пр.
Уровень приемлемой цены зависит как от уровня доходов, так и от силы мотивации, которая привела к решению о покупке.
На принятие решения о выборе конкретного лекарственного средства обычно влияют:
- рекомендации врача;
- рекомендации фармацевта;
- реклама;
- отношение к производителю;
- рекомендации родственников и знакомых.
При наличии данных о заболеваемости с учетом возраста и пола населения возможно установить поправочные коэффициенты для расчета количества приобретаемого лекарственного средства. Эти коэффициенты с достаточной точностью можно получить посредством анкетирования посетителей аптек. При назначении препаратов врач также учитывает пожелания пациентов, отдающих предпочтение тем или иным препаратам для лечения различных заболеваний (рис. 7.41, 7.42). Эти предпочтения также могут быть учтены путем анкетирования врачей.
Анализ данных анкет позволяет определить требуемые коэффициенты предпочтения или мотивации и наиболее перспективные воздействия на потенциального покупателя.
Таким образом, объем рынка может быть определен следующим образом:
- ОР = 0,1ґП + 0,8ґПґ(a + (1–a)ґg),
где ОР — объем рынка; П — потребность в препарате; a — доля потребности для детского лечения; g — коэффициент мотивации.

После этого можно оценить объем рынка при наличии конкурентов.
Для этого необходимо разделить полученный объем рынка на сектора, которые будут принадлежать отдельным лекарственным средствам — аналогам по структуре или механизму действия. С этой целью строится рейтинг препаратов с учетом не только лечебных и потребительских свойств, но и экономических (цена, активность рекламной кампании, наличие сети распространения лекарственного средства и т.д.). Показатели4 и их значимость можно определить, анализируя фактическое состояние рынка препаратов, характеристики этих препаратов и действия соответствующих фирм по продвижению препаратов на рынке. Подробно вопросы построения рейтинга см. 7.6[6]. Обычно рынок делится таким образом, что 20% владеют 80% (принцип Парето). При этом распределение долей имеет характерную убывающую экспоненциальную зависимость в соответствии с предположением F.E. Satterthwaite (см. рис. 2.19). После расчета рейтинга можно определить потенциальный объем рынка с учетом указанного распределения и значения рейтинга лекарственного средства.
Поскольку ряд параметров (цена, лекарственные формы, рекламная кампания и др.) может изменяться, желательно рассчитать варианты для установления возможного интервала размера сектора рынка.
Размер сектора рынка затем может быть определен по формуле
- Сi = ОРґ(1 — Рi ґf/eka),
где Сi — размер сектора рынка для лекарственного средства; ОР — объем рынка; Рi — рейтинг лекарственного средства; f — нормирующий коэффициент; k — номер лекарственного средства в рейтинге; a — коэффициент, зависящий от «крутизны» убывания зависимости (определяется эмпирически в зависимости от степени ориентирования рынка на один препарат).
Нормирующий коэффициент находят из условия:
Точность оценки размера сектора рынка зависит от правильности подбора показателей, характеризирующих конкурентоспособность лекарственного средства, и их относительной значимости. Обычно это осуществляют с участием экспертов, с применением специальных программных средств для анализа экспертных оценок и расстановки значимости критериев.
Для обработки экспертных оценок, составления рейтинга препаратов и моделирования параметров рейтинга при изменении параметров используют программное средство OptimeChoice, функционирующее в среде Windows и написанное на языке С++.
Расчет потребности в лекарственном препарате можно выполнить следующим образом:
где j — год, на который выполняется расчет; i — заболевание, при котором можно использовать препарат; N — количество заболеваний, для лечения которых может использоваться препарат; Зij — уровень заболеваемости по i-й нозологической единице, для j-го года (определяется по методике, описанной в 7.3); Hj — прогноз роста населения на j-й год; Ci — наличие этого препарата в схеме лечения данного заболевания и его место (основной или препарат замены); gi — коэффициент предпочтительности данного лекарственного средства врачами при назначении для лечения данного заболевания; Ki — количество препарата для лечения одного больного (курсовая доза).
Если препарат не имеет аналогов (или рассчитывают потребность на группу препаратов-генериков), gi = 1. В противном случае gi подлежит определению. Наиболее точно этот коэффициент можно определить с помощью анкетирования врачей.
Ki может быть определено несколькими способами:
- из схем лечения, если в них указаны курсовые дозы;
- посредством анкетирования врачей по данной нозологической единице;
- путем получения оценки по данным архивов МЗ об уровне заболеваемости и расходах препаратов в период до 1991 г.
Вариант получения этого коэффициента может быть выбран в зависимости от конкретного лекарственного средства и заболевания, а также от возможности получения требуемых данных.
Рассчитанная таким образом потребность, которая основана на уровне заболеваемости, является теоретической. Она будет совпадать с реальным расходом препаратов только в тех случаях, когда лечение полностью оплачивает государство, во всех остальных случаях реальное потребление лекарственного средства необходимо определять с учетом экономических параметров, то есть фактически определять размер сектора рынка для него.
Предложенный подход позволяет решать как прямую (определение рынка), так и обратную задачи (то есть по фактическому распределению уровня продаж лекарственных средств, их характеристикам, направлениям и уровням рекламного воздействия фирм, их продающих, а также определить фактическую значимость отдельных параметров оценки лекарственного средства и характеристик его продвижения на рынок).
Литература, рекомендуемая к изучению
- Исикава К. Японские методы управления качеством: Сокр. пер. с англ. / Науч. ред. и авт. предисл. А.В. Гличев. — Ч. 1. — М.: Экономика, 1988. — 215 с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка. — К.: ЗАО “Укрспецмонтажпроект”, 1999. — 312 с.
- Макино Т., Осахи М., Докэ Х., Макино К. Контроль качества с помощью персональных компьютеров / Пер. с яп. — М.: Машиностроение, 1991. — 224 с.
- “Семь инструментов качества” в японской экономике. — М.: Изд-во стандартов, 1991. — 88 с.
- Статистические методы повышения качества / Пер. с англ.; Под ред. Х. Кумэ — М.: Финансы и статистика, 1990. — 304 с.
- Старостіна А.О. Маркетингові дослідження. Практичний аспект. — К.; М.; СПб.: Вильямс, 1998. — 262 с.
[1] Олейников Д. Препараты ранитидина: динамика цен. — Еженедельник Аптека, 2000, № 5. — С.8.
[2] Олейников Д. (2000) Препараты ранитидина: динамика цен. Еженедельник Аптека, 5:8.
[3] Нет такого закона, который удовлетворял бы всех (лат.).
[4] GCP рекомендует применять их для контроля любого оборудования, применяемого для измерения данных, используемых в медицине и фармакологии.
[5] Картиш А.П., Середа П.І., Лапач С.М. Розробка методів оцінки об`єму ринку для препаратів // Ліки України.— 1998.— № 3.— С. 26-27.
Середа П.І, Лапач С.М., Чубенко А.В. Аналіз ринку життєво-необхідних лікіарських засобів за допомогою анкетування аптек // Фармакологічний вісник.— 1999.— № 1.— С.76–79.
[6] Лапач C.Н., Чубенко А.В. Применение многокритериальной оптимизации для сравнения препаратов-аналогов // Информационные технологии и программно-аппаратные средства в медицине, биологии и экологии / Материалы семинара, часть 3.— К.: Мединформ, 1998.— С. 38–40; Chubenko A.V., Nijeradze T.I., Lapach S.N. Multicriteria Modeling Methods for Assessment of Requerements in Medicines for the Countries with Transion Economics // 9-th World Congress of Medical Information.— Seoul, 1998; A. Tchubenko, S.M. Lapach, T.I. Nizheradze Multicriteria Modeling Methods for Assessment of Requirements for Drugs // 1998 Western MultiConference, Health Servise Reseach.— SanDiego, 1998; А.В. Чубенко, С.Н. Лапач Рейтинг (отбор) наиболее эффективных лекарственных средств и системы прогнозирования потребности в них // Сб. Проблемы реформирования системы здравоохранения Украины: обеспечение лекарственными препаратами / Материалы IV международной конференции.— Ялта, 1997.— С. 27-31.